Leading Organizations Trust DataRobot.
Explore Customer StoriesDATAROBOT AI PLATFORM
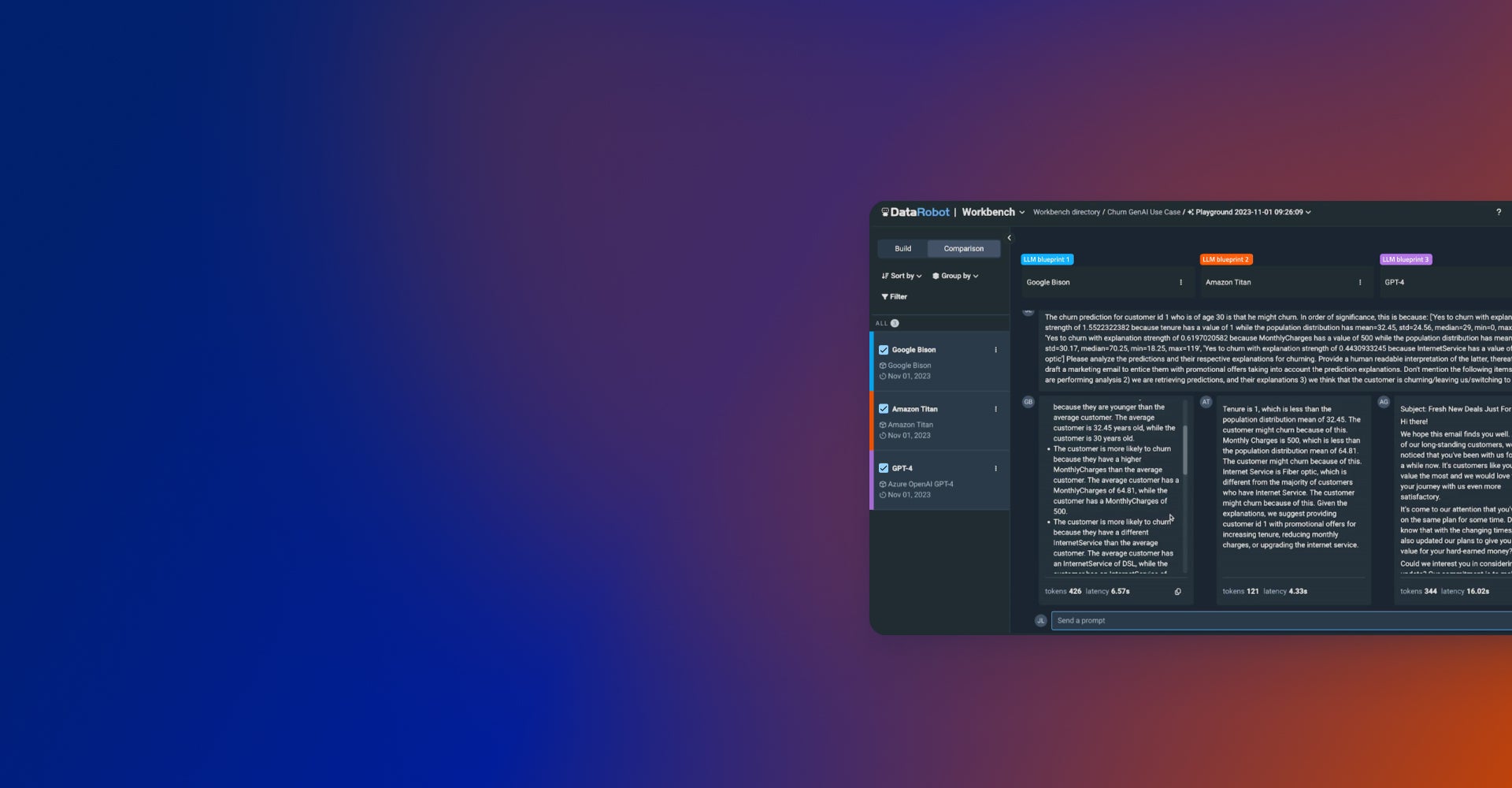
One Unified Platform for Generative and Predictive AI
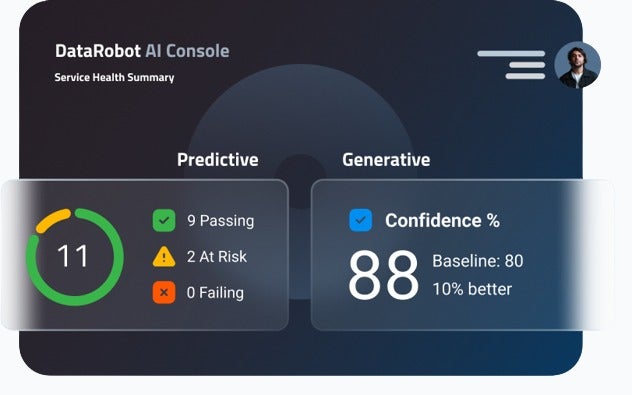
Operate with Confidence
Confidently scale AI and drive business value with unparalleled enterprise monitoring and control.
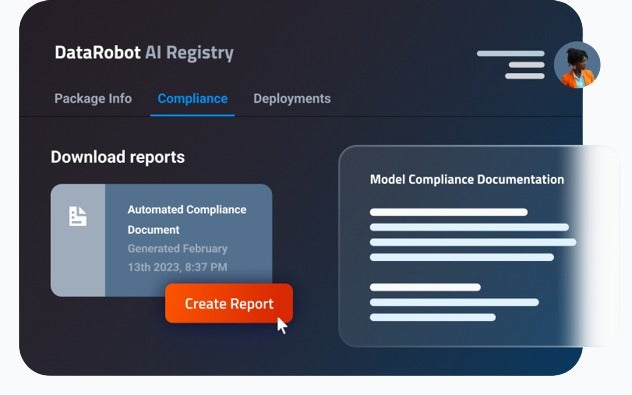
Govern with Full Visibility
Unify your AI landscape, teams, and workflows for full visibility and oversight at scale.
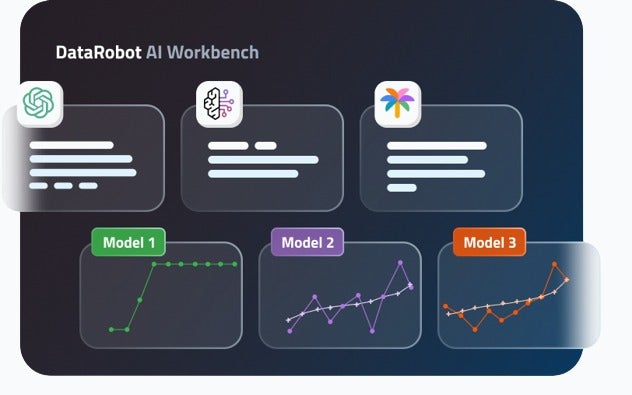
Build with Agility
Innovate rapidly with an open AI ecosystem that gives you the freedom to adapt as needs evolve.
83%
Faster Deployment
4.6X
Return on Investment
80%
Lower Cost
Enterprise Strategy Group (ESG), a division of TechTarget
DEEP ECOSYSTEM INTEGRATIONS
The Most Open AI Platform to Build, Scale, and Adapt with Ease
Explore the DataRobot Difference1 million+
AI projects successfully delivered across a wide range of industries
1000+
customers served, including Fortune 50 companies
10+ years
of platform innovation and real-world
use-case experience
ANALYST REPORTS
Recognized As a Leader By Industry Experts